COVID-19 și problema testelor fals pozitive
După cum e bine cunoscut, numărul raportat de cazuri COVID-19 se bazează pe testul PCR (polymerase chain reaction). Pe lângă acesta mai există și testul serologic, prin care sunt detectați anticorpii care indică o infectare trecută cu coronavirus, dar acesta nu intră în discuția de față. Ceea ce se poate constata în ultimele săptămâni e pe de-o parte o creștere tot mai accentuată a numărului de teste PCR, iar pe de altă parte numărul cazurilor noi de COVID-19 care apar zilnic este practic în scădere, oscilând de câtăva vreme între 120-200 (a se vedea și imaginea de mai sus, unde e reprezentată o zecime din numărul de teste, pentru o mai bună vizualizare comună a ambelor curbe, iar cazurile și testele sunt cumulate pe câte 2 zile). Multe din aceste cazuri se dovedesc a fi asimptomatice, dacă nu chiar fals pozitive. Ce înseamnă de fapt această constatare? Dacă ținem cont de marja de eroare a testelor, faptul nu indică altceva decât că în România și în majoritatea țărilor europene pandemia COVID-19 se apropie de final, că majoritatea cazurilor raportate sunt de fapt fals pozitive și că mai pot exista cel mult focare izolate, ici și colo, dar nu mai poate fi vorba de o răspândire a bolii pe scară largă.
Pentru a ilustra ce se întâmplă, să considerăm pentru moment exemplul unui test ipotetic, care are sensibilitatea de 99% (cazuri pozitive detectate corect) și specificitatea tot de 99% (cazuri negative detectate corect). Prin urmare, 1% din rezultatele testărilor vor fi fals pozitive, aceasta chiar în cazul în care prevalența (proporția celor cu adevărat infectați) ar fi egală cu zero. Aceasta ar fi deja o situație limită, în care nu s-a ajuns încă, dar nici nu mai e foarte departe până acolo. Dar înainte de a discuta cazul concret al testului PCR și statisticile cazurilor pozitive în funcție de numărul de teste, să urmărim următorul exemplu, pentru o mai bună înțelegere a fenomenului și de către cei nefamiliarizați cu aceste noțiuni elementare de statistică și teoria probabilităților. Voi încerca deci în mod deliberat să fac o prezentare cât mai accesibilă și cât mai puțin specializată.
Să presupunem că avem o populație de N=10.000 persoane supusă testului nostru ipotetic, din care 1000 sunt infectate (prevalență de 10%). 99% din acestea, adică 990, vor fi identificate ca atare în mod corect, în vreme ce 1%, adică 10, vor fi raportate fals ca negative. Din cele 9000 de persoane sănătoase, vom avea 8910 (99%) raportate corect negative, dar și 90 (1%) ca fals pozitive. Numărul total de teste pozitive este așadar 990+90=1080, în vreme ce numărul celor infectați este doar 1000. Raportul dintre cele două numere, 1000/1080 este egal cu 0,926, adică peste 9 din 10 teste pozitive sunt corecte.
Pentru a fi mai precis, pentru cunoscători ar fi de adăugat că probabilitatea condiționată P(I|+) de a fi infectat dacă testul a dat un rezultat pozitiv se calculează cu teorema lui Bayes, înmulțind raportul anterior cu sensibilitatea testului, care e de 0,99, rezultatul fiind 0.9166. Din moment ce sensibilitatea e de regulă foarte aproape de 1 (sau de 100%), diferențele nu vor fi semnificative, deci pentru ilustrare putem păstra raportul dintre cei cu adevărat infectați și cei testați pozitiv.
Considerând acum prevalența de 1% (adică 100 de infectați din 10.000) vom obține 99 de teste corect pozitive și tot atâtea fals pozitive, ceea ce duce la un raport de 1:2, iar la o prevalență de 0,2% (20 de infectați din 10.000) vom avea 20 de teste corect pozitive și 100 fals pozitive, adică doar 1 din 6 teste pozitive e de fapt corect. Rezultatele acestui mic calcul sunt sintetizate în tabelul de mai jos.
Concluzia care se desprinde e clară: pe măsură ce prevalența scade, procentajul testelor fals pozitive crește substanțial, la un moment dat ajungându-se la situația în care o majoritate importantă a cazurilor raportate drept pozitive să fie de fapt fals pozitive. Iar dacă numărul absolut al testelor va fi suficient de mare, și numărul absolut al testelor fals pozitive va fi pe măsură, încât un guvern care ia doar aceste date drept criteriu (sau pretext) al acțiunilor sale, va putea decreta o stare de pandemie perpetuă. Cu atât mai mult cu cât e de presupus că virusul nu va dispărea niciodată definitiv din peisaj și întotdeauna va exista un număr (fie el și mic) de cazuri COVID-19 reale, iar nu fals pozitive.
Bineînțeles, în practică testarea nu se face (sau nu ar trebui să se facă) la voia întâmplării, mai ales în cazurile unei prevalențe scăzute, când un test pozitiv devine aproape irelevant. Profesioniștii în domeniu cunosc desigur acest lucru și își adaptează strategia testărilor în consecință. Din moment ce la o prevalență ridicată informația dată de rezultatul pozitiv al testului e mult mai acurată, ei vor testa doar acele grupuri unde se așteaptă la mai multe rezultate pozitive, așa cum și pescarul experimentat nu-și aruncă undița la nimereală, ci în locurile în care se așteaptă să muște peștele.
Astfel, e logic să fie testat personalul medical, care intră zilnic în contact cu bolnavii de COVID-19 și unde riscul de contaminare e unul real. Un alt grup important e format din persoanele cu simptome tipice. Aici rezultatul testului e foarte probabil să fie unul pozitiv, caz în care urmează a fi testați și cei care au intrat în contact cu persoana în cauză, membri ai familiei, colegi de muncă, prieteni, etc. Dacă există un caz cert, pe lângă care mai sunt testate de exemplu încă 50 de persoane, în cadrul acestui grup avem deja o prevalență de cel puțin 2% (1 din 50 e infectat cert). Dacă sunt 2 din 50, prevalența crește deja la 4%, caz în care alte rezultate pozitive ale testului vor avea o probabilitate semnificativă de a fi și corecte. Dacă însă aruncăm undița testului la întâmplare și testăm fără motiv 50 de persoane selectate aleator, vom găsi probabil printre ele una care e fals pozitivă și cam atât – repet, în condițiile în care prevalența la nivelul întregii societăți e foarte mică, la nivelul zecimilor de procent.
Prin urmare, e lipsit de sens să sporești numărul testelor PCR aplicându-le nediferențiat unei mari părți a populației, după cum în mod corect a sesizat și dl. Vlad Mixich ca răspuns la ideea Gabrielei Firea de a-i testa pe bucureșteni. Tot nonsens e prin urmare și propunerea, fie ea bine intenționată, de a testa la grămadă elevii și profesorii din școli. Dacă ar exista bănuieli întemeiate, bazate pe cazuri simptomatice, sau indicii că prevalența în rândul acestui grup ar fi măcar de peste 1%, atunci da, testarea are avea sens, dar diferențiat, doar în unitățile de învățământ în cauză. Căci altfel, în lipsa unei prevalențe suficiente, rezultatul acestei campanii de testare nu ar fi decât un număr mare de cazuri fals pozitive, cu toate consecințele care decurg de aici: internarea forțată pe secții alături de bolnavi reali, probabil închiderea școlilor în cauză, etc. Adică panică și isterie gratuită!
Altfel stau lucrurile în cazul testului serologic, care detectează anticorpii dobândiți ca urmare a trecerii prin boală. În primul rând aici prevalența e de așteptat să fie mult mai mare, iar în al doilea rând un rezultat fals pozitiv nu implică nicio tragedie, ci cel mult un fals sentiment de siguranță. Efectuarea unor astfel de teste pe scară largă nu e prin urmare la fel de problematică.
O altă situație în care testarea are sens e aceea în localitățile care s-au remarcat drept focare de COVID-19 și unde prevalența e de așteptat să fie mai ridicată. În România un astfel de exemplu îl reprezintă orașul Suceava, unde chiar se desfășoară o asemenea campanie de testare. Din probele analizate până acum, în număr de 240, 11 cazuri au fost pozitive la testul PCR (4,5%), iar 43 pozitive la testul serologic. Folosind parametrii testului ca fiind cei de mai sus (specificitate și sensibilitate de 99%, vom vedea mai încolo că valorile reale sunt apropiate, dar ceva mai scăzute), putem calcula prevalența, adică numărul real al celor infectați, evident, la nivel de probabilitate, x=P(I)*240 . Anume: 11=0,99*x+0.01*(240-x) (adunăm 99% teste corect pozitive și 1% teste fals pozitive pentru a obține cele 11 teste pozitive). Rezultatul este x=8,775 (adică e de așteptat ca din cele 11 teste, două să fie fals pozitive, iar acest număr x raportat la numărul 240 de teste dă o prevalență de circa 3,6%). Pentru a calcula așadar probabilitatea condiționată P(I|+) de a fi cu adevărat infectat, dacă rezultatul testului a fost pozitiv, vom considera x/11 (similar cu penultima coloană din tabelul de mai sus) și vom înmulți cu sensibilitatea de 0,99 (teorema lui Bayes, similar cu ultima coloană din tabel), obținând P(I|+)=0,79, așadar probabilitatea ca cineva din cei 11 testați pozitiv să fie cu adevărat infectat este de 79%. Trebuie remarcat însă că s-a testat pe bază de voluntariat, deci iarăși nu pe un eșantion ales la întâmplare, iar la test s-au prezentat persoane care probabil au avut motive să considere că sunt potențial infectate, prin contact cu alte cazuri deja validate, etc. Prin urmare, nu e vorba de un eșantion reprezentativ, iar la nivelul orașului Suceava nu putem vorbi de 3,6% din populație infectată activ cu coronavirus, ci de un procentaj mult mai mic.
Scopul principal al acestui text e să analizeze de fapt situația la nivelul întregii țări. Pentru aceasta avem nevoie de statisticile privind cazurile de COVID-19 înregistrate zilnic dar și numărul zilnic de teste efectuate, pentru a putea determina procentajul testelor pozitive, așa ca în exemplul de mai sus. Aceste date pot fi preluate de pe statista.com, sub linkurile date la începutul acestui articol. După cum s-a văzut, e nevoie și de parametrii reali ai testului PCR, care pot fi găsiți aici: (e vorba de un raport de validare a testului realizat de un institut de specialitate din Germania). Anume, sensibilitatea este de 98,8% iar specificitatea de 98,6% (deci ambele aproape de valorile de 99% din exemplele ilustrative de mai sus, ale căror rezultate rămân practic valabile și cu noile numere). Mai mult, dacă în absența oricărui virus, testul PCR dă un procentaj de 1,4% de teste fals pozitive, în prezența unor alți viruși din familia corona (care cauzează de pildă răceli banale), procentajul fals pozitiv crește la 7,6%, dar voi ignora acest aspect și voi rămâne la cifrele de peste 98%.
Aplicând același raționament pe care l-am exemplificat în cazul testelor din Suceava la datele din întreaga țară, rezultatul e reprezentat în următoarea diagramă.
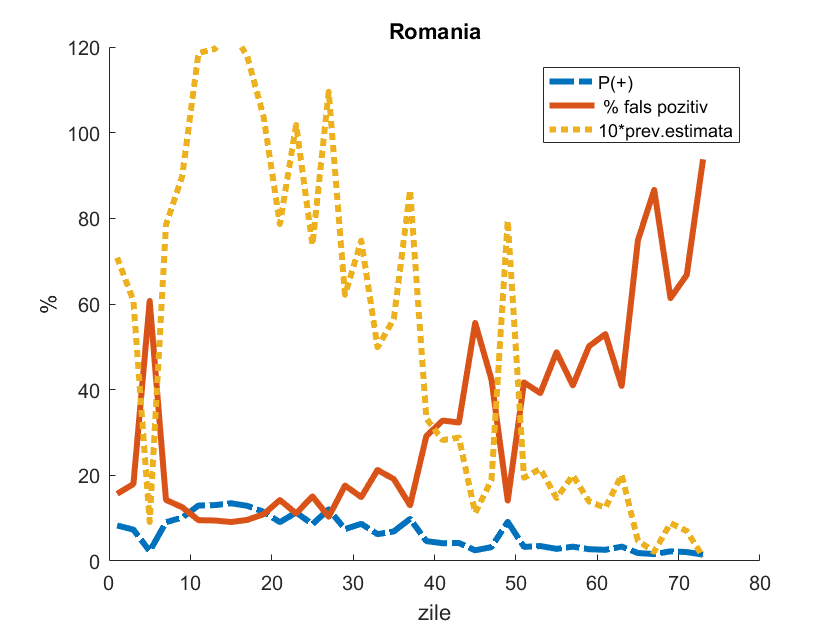
Curba prevalenței estimate e situată de fapt tot timpul puțin sub cea a procentajului testelor pozitive, de aceea pentru o mai bună citire a valorilor e reprezentată înmulțită cu factorul 10. În ultima săptămână procentajul testelor pozitive se mișcă între 1,5%-2%, iar prevalența estimată e în permanență sub 1% , cea mai recentă valoare fiind de 0,1% (valoarea de la capătul curbei). Raportat la aceasta, probabilitatea ca cineva testat pozitiv să fie cu adevărat infectat e de doar 6,3%, ceea ce implică faptul că mai bine de 9 din 10 din testele pozitive sunt de fapt fals pozitive (curba roșie P(S|+) calculată cu teorema lui Bayes). E de reținut că această prevalență de 0,1% nu e raportată la întreaga populație a României, ci la nivelul grupelor considerate a fi mai expuse, adică acelea indicate de strategia testelor, așa cum am exemplificat mai sus. Încet, în ciuda creșterii numărului de teste, ne apropiem tot mai mult de marja de eroare a testului, de acele 1,4% fals pozitive care ar apărea chiar și în cazul în care numărul real de infecții ar fi zero.
Diagrama cu datele României începe pe data de 14 martie. În primele 40-45 de zile ale intervalului de timp în discuție, deci aproximativ până la sfârșitul lui aprilie, probabilitatea testelor fals pozitive a fost relativ scăzută, sub 20%. Dar odată cu luna mai, aceasta a început să crească, de la 40%, ajungând chiar la 80%, scăzând ulterior iar, dar cea mai recentă valoare este de circa 92,7%. Evident că există și fluctuații, trendul general e însă clar, încât putem bănui ce va urma în perioada următoare.
Aceasta o putem vedea și în Germania, unde pandemia a izbucnit cu aproximativ două săptămâni în avans. Aici Institutul Robert Koch raportează statisticile săptămânale ale numărului de teste și procentajului celor pozitive (faptul că e vorba de statistici săptămânale explică aspectul mai neted al curbelor). Astfel, între 18-24 mai s-au efectuat 344.782 de teste, din care doar 1,5% au fost pozitive. Aplicând aceleași calcule ca mai sus, rezultatul va fi că prevalența estimată e de doar 0,1% (repet: în cadrul grupelor de risc, unde se testează, nu la scara întregii populații), iar probabilitatea unui test fals pozitiv a ajuns la 97,3%!
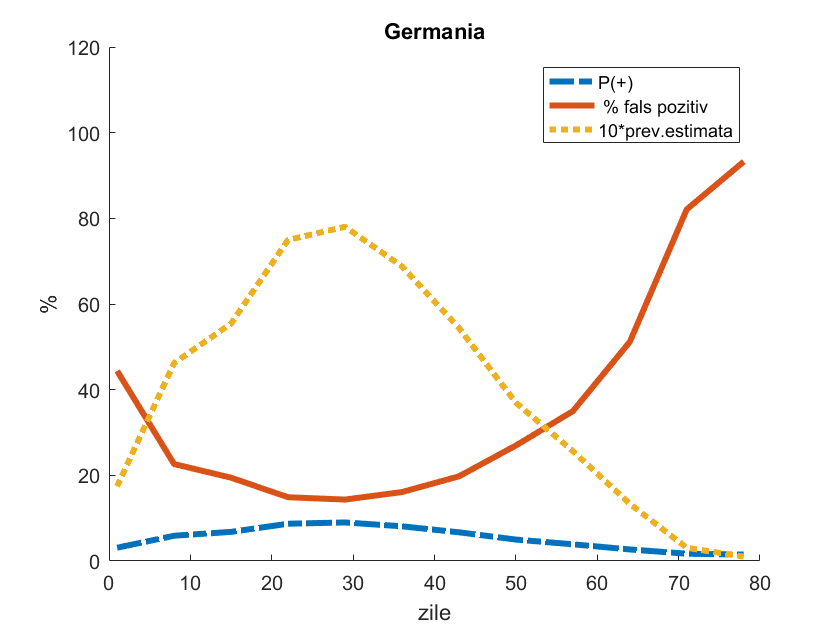
Cum spuneam, coronavirusul probabil nu va dispărea niciodată complet. Focare izolate se vor găsi în permanență, deci va exista mereu și un număr de teste corect pozitive. Dar atunci când la nivelul unei țări întregi procentajul testelor pozitive se apropie tot mai mult de procentajul de fals pozitive pe care l-am avea chiar în absența completă a virusului, concluzia se impune de la sine: ar trebui decretat sfârșitul stării de pandemie! Boala mai există, prin câte un focar izolat, ici și colo, dar acest nu poate influența tabloul general, căci cifrele nu mint. Cert este faptul că răspândirea pe scară largă nu mai există.
Faptul că majorității politicienilor care conduc țările lumii le convine această stare de pandemie perpetuă (pe care, dacă vor, o pot întreține în permanență printr-un număr suficient de mare de teste, majoritatea fals pozitive, pe lângă mediatizarea puternică a puținelor cazuri reale), la adăpostul căreia se pun la cale ample transformări politice și sociale, e altă poveste, care merită o discuție separată.
ActiveNews nu a primit niciodată altă publicitate decât cea automată, de tip Google, din care o îndepărtăm pe cea imorală. Aceasta însă nu ne asigură toate costurile.
Ziarele incomode sunt sabotate de Sistem. Presa din România primeste publicitate (adică BANI) doar în măsura în care este parte a Sistemului sau/și a Rețelei Soros. Sau dacă se supune, TACE sau MINTE.
ActiveNews NU vrea să se supună. ActiveNews NU vrea să tacă. ActiveNews NU vrea să mintă. ActiveNews VREA să rămână exclusiv în slujba Adevărului și a cititorilor.
De aceea, are nevoie de cititorii săi pentru a supraviețui așa cum este acum. Dacă și tu crezi în ceea ce credem noi, te rugăm să ne sprijini să luptăm în continuare pentru Adevăr, pentru România!
RO02BTRLRONCRT0563030301 (lei) | RO49BTRLEURCRT0563030301 (euro)
Pe același subiect

De la ”Vaccinare în viteza a șasea”, la Terapie Intensivă. Mihai Leu, în stare critică la Spitalul Fundeni din București. Fostul campion la box și raliuri a fost transportat de urgență cu elicopterul

Robert F. Kennedy: ”Gardasil este probabil cel mai rău vaccin în masă pe care l-am văzut vreodată”

Celebra actriță Teddi Mellencamp este în fază terminală de cancer generalizat, la 43 de ani, după ce s-a vaccinat Covid în 2021

Mort subit după vaccin, în floarea vieții - a debutat post-mortem...

Colegiul Pseudo-Medicilor reîncepe prigonirea Medicului Răzvan Constantinescu după ce acesta a ridicat problema MORȚILOR SUBITE din rândul cadrelor medicale în urma vaccinării cu seruri experimentale Covid. ”Abia aștept să-i umilesc din nou!”

Slovacia lansează o anchetă privind vaccinul Covid-19 după constatările de contaminare cu ADN
Recomandările noastre

22 aprilie 1990, startul Pieței Universității. În urmă cu 35 de ani începea cea mai amplă manifestație anticomunistă din Europa Centrală și de Est. VIDEO și GALERIE FOTO


 O comparație între gripa sezonieră și Covid-19
O comparație între gripa sezonieră și Covid-19 

Autentifică-te sau înregistrează-te pentru a trimite comentarii.
Comentarii (0)